This site is made possible by member support. ❤️
Big thanks to Arcustech for hosting the site and offering amazing tech support.
When you buy through links on kottke.org, I may earn an affiliate commission. Thanks for supporting the site!
kottke.org. home of fine hypertext products since 1998.
Mathematician Terence Tao won both the Fields Medal and a MacArthur genius grant last year. To dumb it down for all you Fields Medal non-winners out there, that’s like doing Miss America and Miss Universe at the same time.
On March 14, 1998, I made the first post to this little site. And I’m still standin’ (yeah yeah yeah). Here’s to 9 more years. Actually, I’ll settle for making it to 10. Baby steps.
In addition to my regular duties on kottke.org, I’m editing Buzzfeed today. Stories so far: Bracket Madness, Sweet Sweet Passover Coke, and 2007 Movie Season. More to come this afternoon.
And if that weren’t enough excitement for one day, it’s also Pi Day. (Whoa, the Pi Day web site uses Silkscreen!) I bet the Pi Dayers are really looking forward to 2015 when they can extend the fun to two additional decimal places.
The Golden Ratio and its appearance in the music of Nintendo’s Zelda games.
A list of distinctive numbers and why they’re so special.
Update: Then again, maybe every number is interesting. (thx, edmund)
Rule of thumb to avoid photographing people with their eyes closed: divide the number of people by three (or by two if the light is bad). That means that if you’re taking a photo of 12 people, you need to take at least 4 photos to have a good chance of getting a photo with everyone’s eyes open. (via photojojo)
Update: Jeff writes: “Way back when we only used film I learned you could tell before looking at the photo whether someone blinked by asking them what color was the flash. If it was white or bluish white, then their eyes were open. If it was orange, then their eyes were closed and they had ‘seen’ the flash through their eyelids.”
Formulas for writing reviews of music, restaurants, and boutique clothing stores (???). “What the a lacked in x, the b made up for in y. Where a = a menu item, x = a characteristic often used in conjunction with fast cars, b = a menu item, and y = an adjective generally used by Victorian novelists to describe a young woman.” (via airbag)
Tupper’s Self-Referential Formula is an equation that when graphed, displays the formula itself.
Update: In computing, a quine is a program which “produces its complete source code as its only output”. (thx, sam)
A look at Saks Fifth Avenue’s new logo and identity. The identity system consists of cutting up the logo into patterns….98,137,610,226,945,526,221,323,127,451,938,506, 431,029,735,326,490,840,972,261,848,186,538, 906,070,058,088,365,083,852,800,000,000,000 possible patterns.
Here’s the 3129 character code you need to enter into a car’s keyless entry pad in order to guess the 5-digit passcode. It’ll take you 20 minutes or less to enter it. (via j-walk)
Hmm, perhaps Richard Taylor’s fractal analysis of Jackson Pollock paintings isn’t that useful after all.
Slashdot recently crossed 16,777,216 (that’s 2^24) comments, after which no more could be added because of a database misconfiguration. (via waxy)
What’s so special about the number 1729? (Turns out, quite a lot.)
On the heels of the possible proof of the Poincare conjecture, another of the $1 million Clay Institute Millennium Prize problems has possibly been proven: the Navier-Stokes equations. The paper is available here.
Update: Oops, “This paper is being withdrawn by the author due a serious flaw.” (thx, tj)
Last month I covered the hubbub surrounding the still-potential proof of the Poincare conjecture. The best take on the situation was a New Yorker article by Sylvia Nasar and David Gruber, detailing the barest glimpse of the behind-the-scenes workings of the mathematics community, particularly those involving Grigory Perelman, a recluse Russian mathematician who unveiled his potential Poincare proof in 2002 and Shing-Tung Yau, a Chinese mathematician who, the article suggested, was out for more than his fair share of the credit in this matter.
After declining the Fields Medal, the Nobel Prize of mathematics, Perelman has quit mathematics and lives quietly in his native Russia. Yau, however, is upset at his portrayal (both literally and literary) in the New Yorker article and has written a letter to the New Yorker asking them to make a prominent correction and apologize for an illustration of Yau that accompanied the article. From the letter:
I write in the hope of enlisting your immediate assistance, as well as the assistance of The New Yorker, in undoing, to the extent possible, the literally world-wide damage done to Dr. Yau’s reputation as a result of the publication of your article. I also write to outline for you, on a preliminary basis, but in some detail, several of the more egregious and actionable errors which you made in the article, and the demonstrably shoddy “journalism” which resulted in their publication.
The letter, addressed to the two authors as well as the fact-checker on the article and CC’d to David Remnick and the New Yorker’s general counsel, runs 12 pages, so you may want to have a look at the press release instead. A webcast discussing all the details of the letter is being held at noon on September 20…information on how to tune in will be available at Dr. Yau’s web site. (thx, david)
A short interview with Grigory Perelman, the Russian mathematician who proved the Poincare conjecture and turned down the Fields Medal. “Newspapers should be more discerning over who they write about. They should have more taste.” (thx pedro)
As I mentioned yesterday, the New Yorker published an article by Sylvia Nasar1 and David Gruber about the recent proof of the Poincare Conjecture2. (Previous coverage in the NY Times and the Guardian.) The article, which is unavailable from the New Yorker’s web site (they’ve now made it available), contains the only interview I’ve seen with Grigory Perelman, the Russian mathematician who published a potential proof of the conjecture in late 2002, gave a series of lectures in the US, and then went back to Russia. Since then, he hasn’t communicated with anyone about the proof, has quit mathematics, and recently refused the Fields Medal, the most prestigious award that mathematics has to offer, saying:
It was completely irrelevent for me. Everybody understood that if the proof is correct then no other recognition is needed.
Meanwhile, a Chinese group of mathematicians, led by Shing-Tung Yau3, are claiming that Perelman’s proof was too complicated and are offering a reworked proof instead of Perelman’s. That is, they’re claiming the first complete proof of the conjecture. Yau The active director of Yau’s mathematics institute explained the relative contributions thusly:
Hamilton contributed over fifty per cent; the Russian, Perelman, about twenty five per cent; and the Chinese, Yau, Zhu, and Cao et al., about thirty per cent. (Evidently, simple addition can sometimes trip up even a mathematician.)
Clearly the Chinese gave more than 100% in solving this proof, but Yau is regarded by some mathematicians as attempting to grab glory that does not belong to him. John Morgan, a mathematician at Columbia University, says:
Perelman already did it and what he did was complete and correct. I don’t seen anything that [Yau et al.] did different.
Yau wants to be associated with the proof of the Poincare Conjecture, to have China associated with it, and for his student, Zhu, to be elevated in status by it. The $1 million in prize money for the proof of the conjecture offered by the Clay Mathematics Institute can’t be far from Yau’s mind as well. For his part, Grigory Perelman won’t say whether he’ll accept the prize money until it is offered. Stay tuned, I guess.
[1] Nasar wrote A Beautiful Mind, a book about mathematician John Nash. ↩
[2] Poincare (properly written as Poincaré) is pronounced Pwan-cah-RAY, not Poyn-care as I said it up until a few weeks ago. ↩
[3] Yau proved a conjecture by Eugenio Calabi which gave birth to a highly useful mathematical structure called a Calabi-Yau manifold; Yau won the Fields Medal for it. The C-Y manifold is important in string theory and Andrew Wiles used it as part of his proof of Fermat’s Last Theorem. In short, Yau is a mathematical stud, no question. ↩
Grigory Perelman, who I posted about last week, has indeed won the Fields Medal for his possible proof of the Poincare Conjecture but declined the award. The current New Yorker has an article (not online) about the whole deal which I have yet to read.
David from Ironic Sans is staying in a New Hampshire residence once owned by Norbert Wiener, a mathematician and the founder of cybernetics and reports back about what’s on Wiener’s bookshelves.
With math immortality, the Fields Medal, and $1 million on the line, an eccentric Russian mathematician comes from out of nowhere, proves the Poincare conjecture, and then disappears again. A whodunnit with thousands of pages of mathematical formulas.
The Wolfram Integrator uses a web version of Mathematica to find integrals of functions. We used Mathematica a lot in college to help visualize examples from math and physics classes. (via rw)
The Biology of B-Movie Monsters, or why you just can’t scale living things up (a la King Kong) or down (like in Fantastic Voyage) without consequence. One key problem: with a theoretical 20 foot tall human, mass increases much faster than bone strength and at some point, his skeleton wouldn’t be able to support the weight.
Works of fiction (books mosly) which deal significantly with mathematics.
A Manchester scientist has come up with a mathematical formula to assess the perfection of the female derriere. “Dr Holmes said that Kylie Minogue, whose celebrated bottom relaunched her career with the help of a pair of hotpants, would almost certainly score a perfect 80.”
Modern mathematical proofs are so complex that it’s becoming impossible to prove them with absolute certainty. About a 1980 proof, an expert says “twenty-five years later we’re still not sure if it’s correct or not. We sort of think it is, but no one’s ever written down the complete proof”. I don’t think I heard my math teachers ever say “sort of”.
Benford’s Law describes a curious phenomenon about the counterintuitive distribution of numbers in sets of non-random data:
A phenomenological law also called the first digit law, first digit phenomenon, or leading digit phenomenon. Benford’s law states that in listings, tables of statistics, etc., the digit 1 tends to occur with probability ~30%, much greater than the expected 11.1% (i.e., one digit out of 9). Benford’s law can be observed, for instance, by examining tables of logarithms and noting that the first pages are much more worn and smudged than later pages (Newcomb 1881). While Benford’s law unquestionably applies to many situations in the real world, a satisfactory explanation has been given only recently through the work of Hill (1996).
I first heard of Benford’s Law in connection with the IRS using it to detect tax fraud. If you’re cheating on your taxes, you might fill in amounts of money somewhat at random, the distribution of which would not match that of actual financial data. So if the digit “1” shows up on Al Capone’s tax return about 15% of the time (as opposed to the expected 30%), the IRS can reasonably assume they should take a closer look at Mr. Capone’s return.
Since I installed Movable Type 3.15 back in March 2005, I have been using its “post to the future” option pretty regularly to post my remaindered links…and have been using it almost exclusively for the last few months[1]. That means I’m saving the entries in draft, manually changing the dates and times, and then setting the entries to post at some point in the future. For example, an entry with a timestamp like “2006-02-20 22:19:09” when I wrote the draft might get changed to something like “2006-02-21 08:41:09” for future posting at around 8:41 am the next morning. The point is, I’m choosing basically random numbers for the timestamps of my remaindered links, particularly for the hours and minutes digits. I’m “cheating”…committing post timestamp fraud.
That got me thinking…can I use the distribution of numbers in these post timestamps to detect my cheating? Hoping that I could (or this would be a lot of work wasted), I whipped up a MT template that produced two long strings of numbers: 1) one of all the hours and minutes digits from the post timestamps from May 2005 to the present (i.e. the cheating period), 2) and one of all the hours and minutes digits from Dec 2002 - Jan 2005 (i.e. the control group). Then I used a PHP script to count the numbers in each string, dumped the results into Excel, and graphed the two distributions together. And here’s what they look like, followed by a table of the values used to produce the chart:
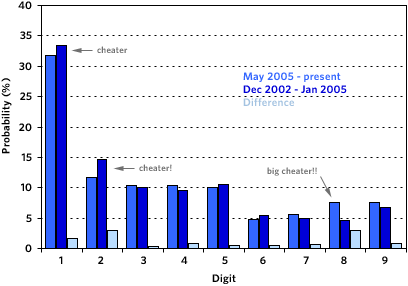
| Digit | 5/05-now | 12/02-1/05 | Difference |
| 1 | 31.76% | 33.46% | 1.70% |
| 2 | 11.76% | 14.65% | 2.89% |
| 3 | 10.30% | 9.96% | 0.34% |
| 4 | 10.44% | 9.58% | 0.86% |
| 5 | 10.02% | 10.52% | 0.51% |
| 6 | 4.83% | 5.40% | 0.57% |
| 7 | 5.66% | 4.96% | 0.70% |
| 8 | 7.62% | 4.65% | 2.97% |
| 9 | 7.60% | 6.81% | 0.79% |
As expected, 1 & 2 show up less than they should during the cheating period, but not overly so[2]. The real fingerprint of the crime lies with the 8s. The number 8 shows up during the cheating period ~64% more than expected. After thinking about it for awhile, I came up with an explanation for the abundance of 8s. I often schedule posts between 8am-9am so that there’s stuff on the site for the early-morning browse and I usually finish off the day with something between 6pm-7pm (18:00 - 19:00). Not exactly the glaring evidence I was expecting, but you can still tell.
The obvious next question is, can this technqiue be utilized for anything useful? How about detecting comment, trackback. or ping spam? I imagine IPs and timestamps from these types of spam are forged to at least some extent. The difficulties are getting enough data to be statistically significant (one forged timestamp isn’t enough to tell anything) and having “clean” data to compare it against. In my case, I knew when and where to look for the cheating…it’s unclear if someone who didn’t know about the timestamp tampering would have been able to detect it. I bet companies with services that deal with huge amounts of spam (Gmail, Yahoo Mail, Hotmail, TypePad, Technorati) could use this technique to filter out the unwanted emails, comments, trackbacks, or pings…although there’s probably better methods for doing so.
[1] I’ve been doing this to achieve a more regular publishing schedule for kottke.org. I typically do a lot of work in the evening and at night and instead of posting all the links in a bunch from 10pm to 1am, I space them out over the course of the next day. Not a big deal because increasing few of the links I feature are time-sensitive and it’s better for readers who check back several times a day for updates…they’ve always got a little something new to read.
[2] You’ll also notice that the distributions don’t quite follow Benford’s Law either. Because of the constraints on which digits can appear in timestamps (e.g. you can never have a timestamp of 71:95), some digits appear proportionally more or less than they would in statistical data. Here’s the distribution of digits of every possible time from 00:00 to 23:59:
1 - 25.33
2 - 17.49
3 - 12.27
4 - 10.97
5 - 10.97
6 - 5.74
7 - 5.74
8 - 5.74
9 - 5.74
Three economists share a cab, getting off at three different destinations. How do they split the fare? For answers, you might look to John Nash or the Talmud.
An investigation into the properties of number spirals (and prime numbers).
Brian Greene on Einstein’s most famous equation, E =mc^2. When he finally gets around to it in the middle of the article, Greene’s got a pretty good layman’s explanation of what the formula actually means.
Freeman Dyson on his friend and colleague Richard Feynman for The New York Review of Books.
Stay Connected